Let be 314 C = 3768 cm b) Work out the circumference of the base of the table Let be 314 C = 942 cm C = 2 × 314 × 15 4) The diameter of a wheel on Kyle's bicycle is 075 m C = 2 × 314 × 0375 a) Calculate the circumference of the wheel C =Steps Involved in Finding Orthocenter of a Triangle Find the equations of two line segments forming sides of the triangle Find the slopes of the altitudes for those two sides Use the slopes and the opposite vertices to find the equations of the two altitudes Solve the corresponding x and y values, giving you the coordinates of the orthocenterFor example, the solution to the equations 2x 3y = 15 and x y = 10 is x = 3 and y = 7 Simultaneous equations are used when trying to find the intersection of two lines (two equations) or three planes (three equations) If any of the equations are equivalent, there will be an infinite number of solutions

Algebraic Elimination Method Class 10 Ncert Solutions Suresolv
X-y=3 x/3 y/2=6 by cross multiplication method
X-y=3 x/3 y/2=6 by cross multiplication method- By Cross multiplication, we get 11x 22 = 9y 18 Subtracting 22 both side, we get 11x = 9y – 4 Dividing by 11, we get x = 9y – 4 / 11 (i) Given that 3 is added to both the numerator and the denominator it becomes 5 / 6 If, 3 is added to both the numerator and the denominator it becomes 5 / 6 (x3) / y 3 = 5 / 6 (ii) By CrossUnlock StepbyStep (x^2y^21)^3x^2y^3=0 Extended Keyboard Examples




Solve By Reducing Them To A Pair Of Linear Equations 5 X 1 1 Y 2 2 6 X 1 3 Y 2 1 Youtube
Now by using cross multiplication we get x/(b 1 c 2 – b 2 c 1) = y/(c 1 a 2 – c 2 a 1) = 1/(a 1 b 2 – a 2 b 1) (1/x)/(6 2) = (1/y)/(2 6) = 1/(1 1) So, x = 1/2 and y = 1/4 Hence, x = 1/2 and y = 1/4 Question 6 ax by = a – b and bx – ay = a b Solution Given that, ax by = a – b bx – ay = a b Or, ax by – (a – b) = 0 bx – ay – (a b) = 0{y = 3 x − 5 x 2 y = 2 6 {y = x 2 x 3 y = 10 7 Typically, we have to find an equivalent system by applying the multiplication property of equality to one or both of the equations as a means to line up one of the variables to eliminate Part A Elimination Method Solve by elimination 1 {x y =Free math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics homework questions with stepbystep explanations, just like a math tutor
0 votes 1 answer Solve for x and y 10/xy 2/xy = 4 ,15/xy9/xy = 2,where x ≠ y, x ≠ ySolution—cross method Factors of 5 y 2 are 5 y and y Factors of 6 are 1 and 6 or 2 and 3 Possible combinations that give a middle term of y 13 are By guessing and checking, we choose the correct combinationSubstitution method review (systems of equations) CCSSMath 8EEC8, 8EEC8b, HSAREIC6 The substitution method is a technique for solving a system of equations This article reviews the technique with multiple examples and some practice problems for you to try on your own
Chapter 7 Rational Expressions 71 Simplifying, Multiplying, and Dividing Rational Expressions Rational Expressions An expression that can be written in the form P / Q , where P and Q are polynomials and Q ≠ 0 Examples 3 x2/18 x2, 7 x/( x2 – 9 ), ( x2 2 x – 15 )/( 4 x ) Fundamental Principle of Reducing Rational ExpressionsNow if you multiply Left hand side by 30 we get 30* (x/6 y/15) = 30*x/6 30*y/15 =5x 2y Now if we multiply Right hand side of the equation by 30 we get 4*30 = 1 Now if we multiply Left hand side of the equation x/3 y/12 =19/4 by 12 we get 12* (x/3y/12) =12*x/312*y/12 x – y = 3 (2) or y – x = 3 (3) On solving equations (1) and (2), We get 2x = 12 ⇒ x = 6 So, y = 3 On solving equation (1) and (3), We get 2y = 12 ⇒ y = 6 So, x = 3 Number = 10x y = 10(6) 3 = 63 or Number = 10x y = 10(3) 6 = 36 ∴ Required number = 63 or 36



1




2 X 2 3y 1 6 And 3 X 2 Y 0 Problem Set 1 Q6 1 Of Linear Equation In Two Variables Youtube
Get NCERT Solutions for Class 5 to 12 here Visit us for detailed chapterwise solutions of NCERT, RD Sharma, RS Agrawal and more prepared by our expert faculties at TopprBefore doing this you can eliminate any possibility that has a common factor from SB 02 at The School of the Art Institute of Chicago The first, λ = 0 λ = 0 is not possible since if this was the case equation (1) (1) would reduce to y z = 0 ⇒ y = 0 or z = 0 y z = 0 ⇒ y = 0 or z = 0 Since we are talking about the dimensions of a box neither of these are possible so we can discount λ = 0 λ = 0 This leaves the second possibility x z = y z x z = y z



Solve The Following Pairs Of Linear Equations By The Substitution Method 3x 2 5y 3 2 X 3 Y 2 13 6 Sarthaks Econnect Largest Online Education Community




Solve By Reducing Them To A Pair Of Linear Equations 5 X 1 1 Y 2 2 6 X 1 3 Y 2 1 Youtube
This calculator can be used to expand and simplify any polynomial expression Transcript Ex 33, 1 Solve the following pair of linear equations by the substitution method (i) x y = 14 x – y = 4 x y = 14 x – y = 4 From equation (1) x y = 14 x = 14 – y Substituting value of x in equation (2) x – y = 4 (14 – y) – y = 4 14 – y – y = 4 14 – 2y = 4 –2y = 4 – 14 –2y = –10 y = (−10)/(−2) y = 5 Putting y = 5 in (2) x – y = 4 x = y 4 xSolve for x Use the distributive property to multiply xy by x^ {2}xyy^ {2} and combine like terms Use the distributive property to multiply x y by x 2 − x y y 2 and combine like terms Subtract x^ {3} from both sides Subtract x 3 from both sides Combine x^ {3} and x^ {3} to get 0 Combine x 3 and − x 3 to get 0




Rd Sharma Solutions For Class 10 Chapter 3 Pair Of Linear Equations In Two Variables




How To Solve Equations With Three Variables By Cross Multiplication Method Quora
Graph{x^33x^29x5 1459, 1726, 856, 736} FIrst determine the interval of definition, then the behavior of first and second derivatives and the behavior ofHow to Check Your Answer with Algebra Calculator First go to the Algebra Calculator main page Type the following First type the equation 2x3=15 Then type the @ symbol Then type x=6 Try it now 2x3=15 @ x=6Solve the system by the substitution method x^2 y^2 = 113 x y = 15 Solve the system by the substitution method x^2y^2=61 xy=1 Solve system by substitution Y=x2 Y=4x1




Ncert Solutions For Class 10 Maths Chapter 3 Pair Of Linear Equations In Two Variables Ex 3 5 Exercise 3 5




Ex 3 5 3 Solve By Substitution And Cross Multiplication Teachoo
(j) x = 3, y = 2 (k) x = 5, y = 2 (l) a = 5, b = 4 Simultaneous Linear Equations Simultaneous Linear Equations Comparison Method Elimination Method Substitution Method CrossMultiplication Method Solvability of Linear Simultaneous Equations Pairs of Equations Word Problems on Simultaneous Linear Equations Word Problems onThe method of Lagrange multipliers can be applied to problems with more than one constraint In this case the optimization function, w is a function of three variables w = f(x, y, z) and it is subject to two constraints g(x, y, z) = 0andh(x, y, z) = 0 There are two Lagrange multipliers, λ1 and λ2, and the system of equations becomesThe simultanous equation calculator helps you find the value of unknown varriables of a system of linear, quadratic, or nonlinear equations for 2, 3,4 or 5 unknowns A system of 3 linear equations with 3 unknowns x,y,z is a classic example This solve linear equation solver 3 unknowns helps you solve such systems systematically




2x Y 2 X 3y 15 By Elimination Method




3x 2 5y 3 2 And X 3 Y 2 13 6 Solve Using Substitution Method Youtube
To solve by substitution, you first need to isolate one of the variables in one equation by itself on one side the equation Let's isolate the x in the second equation x2y=14 Subtract 2y from both sides x=142y Now you can substitute (142y) for the Its exact solution is u (x, y, t) = e − t x 3 y 36We first consider numerical solutions on a regular grid Table 3 displays the numerical errors of the present Kansa method and the FDM It can be observed from the last row in Table 2 that the Kansa method using far fewer nodes achieves higher accuracy than the FDM The Kansa method has a clearly higher convergence rate than Section 43 Double Integrals over General Regions In the previous section we looked at double integrals over rectangular regions The problem with this is that most of the regions are not rectangular so we need to now look at the following double integral, ∬ D f (x,y) dA ∬ D f ( x, y) d A where D D is any region



Cbse 10 Math Cbse Linear Equations In Two Variables Ncert Solutions
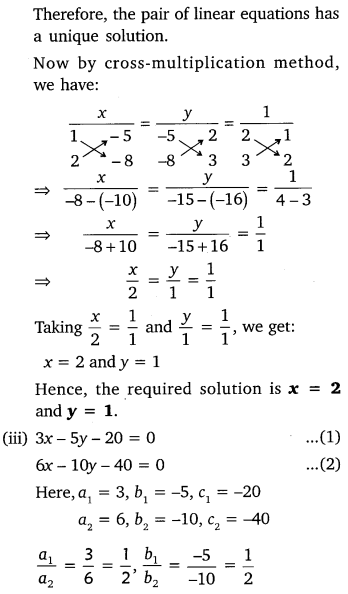



G 1 Coaching Class 3rd Chapter Pair Of Linear Equation In Two Variable
X y = (3 × 1)/ 3 x y = 3 (5) Substitute equation (5) in (1) 3/3 2/ (x – y) = 3 By further calculation 1 2/ (x – y) = 3 2/ (x – y) = 3 – 1 = 2 So we get 2/2 = x – y Here 1 = x – y (6) We can write it as x – y = 1 x y = 3 By adding both the equations 2x = 4 x = 4/2 = 2 Substitute x = 2 in equation (5) 2 y = 3 y = 3 – 2 = 1TYPE/TOPIC OF QUESTIONS SOLVING SIMULTANEOUS EQUATIONS BY SUBSTITUTION METHOD, ELIMINATION METHOD AND CROSSMULTIPLICATION METHOD 1 Use the method of substitution to solve each other of the pair of simultaneous equations (a) x y = 15 x y = Example 17 Solve the pair of equations 2/𝑥 3/𝑦=13 5/𝑥−4/𝑦=−2 2/𝑥 3/𝑦=13 5/𝑥−4/𝑦=−2 So, our equations become 2u 3v = 13 5u – 4v = –2 Hence, our equations are 2u 3v = 13 (3) 5u – 4v = – 2 (4) From (3) 2u 3v = 13 2u = 13




Selina Chapter 6 Linear Equations Including Problems Icse Solutions Class 9 Maths




Solve 3x 4y 10 2x 2y 2 By The Method Of Elimination
Solve for x and y 3/x 6/y = 7, 9/x 3/y = 11 asked Jun 23 in Linear Equations by Hailley (334k points) linear equations in two variables;Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, historyWhatever method helps you consistently complete the simplification correctly is the method you should use Simplify 10 x 3 – 14 x 2 3 x – 4 x 3 4 x – 6 I will start by grouping the terms according to their degree




7 Y 3 2 X 2 14 4 Y 2 3 X 3 2 Youtube




Ncert Class 10 Chapter 3 Pair Of Linear Equations In Two Variables
The given simulattaneous equations are 4xy =3 X2y =3 4x3y3=0 (1) x2y3=0 (2) Fo calculating values of xand y of the given equations cross multiplication mehod is used The method name it self indicates cross multiplication Cross multiplicat3 x – 9 y – 2 =0 (ii) 2 x y = 5 ;Get NCERT Solutions for Class 5 to 12 here Visit us for detailed chapterwise solutions of NCERT, RD Sharma, RS Agrawal and more prepared by our expert faculties at Toppr




Cbse Ncert Solution For Class 10 Maths Linear Equations In 2 Variables




R D Sharma Solutions Class 10th Ch 3 Pair Of Linear Equations In Two Variables Exercise 3 4
(ii) 3/ (x y) 2/ (x – y) = 3 2/ (x y) 3/ (x – y) = 11/3 Solution (i) /(x1) 4/(y–1) = 5 (1) 10/(x1) – 4/(y–1) = 1 (2) Add equation (1) and (2) 30/(x 1) = 6 By cross multiplication ⇒ 30 = 6(x1) By further calculation ⇒ 30/6 = x 1 ⇒ 5 = x 1 So we get ⇒ x = 5 – 1 = 4 Substitute the value of x in equation (1)Solving linear equations using elimination method Solving linear equations using substitution method Solving linear equations using cross multiplication method Solving one step equations Solving quadratic equations by factoring Solving quadratic equations by quadratic formula Solving quadratic equations by completing square In case there is a unique solution, find it by using cross multiplication method (i) x – 3 y – 3 = 0 ;




Algebraic Elimination Method Class 10 Ncert Solutions Suresolv




Ncert Solutions For Class 10 Maths Chapter 3 Exercise 3 5 Pair Of Linear Equations In Two Variables
SOLUTION KEYS FOR MATH 105 HW (SPRING 13) STEVEN J MILLER 1 HW #1 DUE MONDAY, FEBRUARY 4, 13 11 Problems Problem 1 What is wrong with the following argument (from Mathematical Fallacies, Flaws, and Flimflam by Edward Barbeau)To find The solution of the systems of equation by the method of crossmultiplication Here we have the pair of simultaneous equation Rewriting the equation again By cross multiplication method we get And We know that Adding equation (3) and (4) Substituting value of x in equation (3) we get Hence we get the value of and3 x 2 y =8




Which Of The Pairs Of Linear Equations Has Unique Solution No Solution




Systems Of Equations With Elimination X 2y 6 4x 2y 14 Video Khan Academy
A computer algebra system written in pure Python Contribute to sympy/sympy development by creating an account on GitHubSolution For Solve for x and yxy=3,\dfrac x3\dfrac y2=6 HOME BECOME A TUTOR BLOG CBSE QUESTION BANK PDFs MICRO CLASS DOWNLOAD APP Class 10 Math All topics Pair of Linear Equations in Two Variables 523 150 Solve for x and y x − y = 3, 3 xNCERT Solutions for Class 10 Maths Chapter 3 Linear Equations In Two Variables are provided here with simple stepbystep explanations These solutions for Linear Equations In Two Variables are extremely popular among Class 10 students for Maths Linear Equations In Two Variables Solutions come handy for quickly completing your homework and preparing for exams




Solve The Following System Of Equations By Method Of Cross Mult



2x Y 2 X 3y 15 By Elimination Method
Differential equation by deniss G zill 9th edition Enter the email address you signed up with and we'll email you a reset link(A) Main Concepts and Results • Two linear equations in the same two variables are said to form a pair of linear equations in two variables • The most general form of a pair of linear equations is a 1 x b 1 y c 1 = 0 a 2 x b 2 y c 2 = 0, where a 1, a 2, b 1, b 2, c 1,c 2 are real numbers, such that 2 2 22 ab a b11 22 ≠ ≠0, 0 • A pair of linear equations is consistent ifThe addition method of solving systems of equations is also called the method of elimination This method is similar to the method you probably learned for solving simple equations If you had the equation "x 6 = 11", you would write "–6" under either side of the equation, and then you'd "add down" to get "x = 5" as the solutionx 6 = 11 –6 –6




Cross Multiplication Method For Solving Equations A Plus Topper




Ex 3 6 1 I And Ii Solve 1 2x 1 3y 2 1 3x 1 2y
X y 3 ÷ x 2 y 3 x 1 3 × x 5 3 Evaluate 9 2 2 3 1 Simplify 3 x 1 y 2 is a 1 If it is not a 1, other methods such as the cross method or the SPF method can be used Example of SPF method Solve 5 x 2 7x2=0 S – sum What is the polynomial of degree 3 which has 4 as the coefficient of x 3 and x , a coefficientDerivation of Cross multiplication method In general, a pair of linear equations in two variables can be represented as = and = For solving pair of linear equations in two variables following steps are followed Step i) Equation (1) is multiplied with and Equation (2) by Step ii) Subtracting Equation (4) from (3)




Cross Multiplication Method For Solving Equations A Plus Topper




Class 10 Maths Chapter 3 Ncert Notes Download Pdf




Please Help Plz Help I Will Mark As Brilliantsolve By Cross Multiplication Method1 X 2y 1 0 And 2x Brainly In




Which Of The Following Pairs Of Linear Equations Has Unique Solution No Solution Or Infinitely Many Solutions I X 3y 3 0 3x 9y 2 0




Chapter 3 Pairs Of Linear Equations In Two Variables Ncert Solutions For Class 10 Mathematics Cbse Topperlearning




Solve The Following System Of Equations By Method Of Cross Multiplication 2x Y 6 X Y 2




Solving Linear Equations By Cross Multiplication Method X 2y 2 X 3y 7 Brainly In




Mathsmentor Answers Page 30 Ask Truemaths



Solve Each Of The Following Systems Of Equations By The Method Of Cross Multiplication 2x Y 6 0 X Y 2 0 Sarthaks Econnect Largest Online Education Community
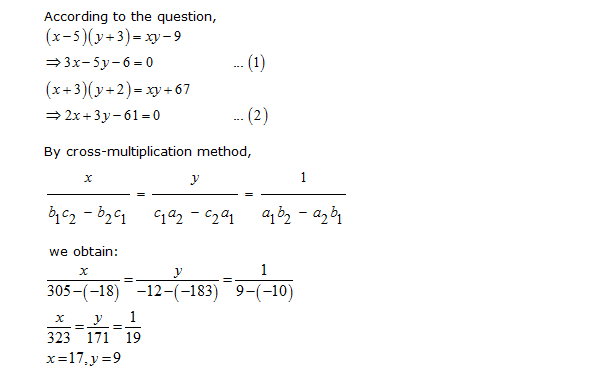



Chapter 3 Pairs Of Linear Equations In Two Variables Ncert Solutions For Class 10 Mathematics Cbse Topperlearning




Ncert Solutions For Class 10 Maths Chapter 3 Pair Of Linear Equations In Two Variables Ex 3 5 Exercise 3 5




Solve The System Of Eq 2x 3y 17 3x 2y 6 By Method Of Cross Multiplication Brainly In




R D Sharma Solutions Class 10th Ch 3 Pair Of Linear Equations In Two Variables Exercise 3 3
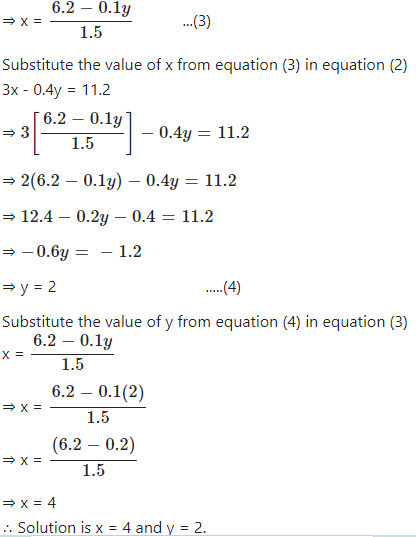



Simultaneous Linear Equations Class 9th Concise Selina Icse Maths Icsehelp



Solve The Following Systems Of Equations 6 X Y 7 X Y 3 1 2 X Y 1 A X Y Where X Y 0 And X Y 0 Sarthaks Econnect Largest Online Education Community




Gseb Solutions For Class 10 Mathematics Pairs Of Linear Equations In Two Variables Cbse Tuts



Q Tbn And9gcqxnk Lpfjle Erogd0wsraw D67yjyrnkghuofquiwt4u Rzfp Usqp Cau



How To Solve 1 X 1 Y 7 2 X 3 Y 17 Where X And Y Is Not Equal To 0 By Cross Multiplication Method Quora



If 2x 3y 17 And 3x 5y 27 What Are X And Y Quora




X 3y 6 2x 3y 12 Solve It In Cross Multiplication Method Ans Step By Step Brainly In




R D Sharma Solutions Class 10th Ch 3 Pair Of Linear Equations In Two Variables Exercise 3 4




Solve The Following System Of Equations By Method Of Cross Mult
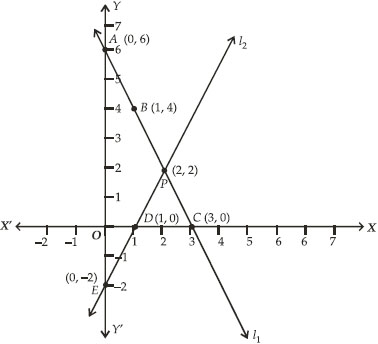



Ncert Solutions Pair Of Linear Equations In Two Variables Class 10
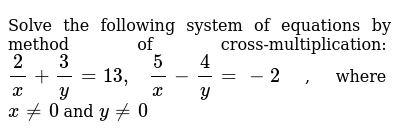



Solve The Following System Of Equations By Method Of Cross Mult



How To Solve The Following Simultaneous Equations By Elimination Method A 2x 3y 12 X Y 1 B 3x Y 10 C X 3y 1 3x 2y 4 0 D 5 Quora



Solve The Following Systems Of Equations 6 X Y 7 X Y 3 1 2 X Y 1 A X Y Where X Y 0 And X Y 0 Sarthaks Econnect Largest Online Education Community



Mfm2p




R D Sharma Solutions Class 10th Ch 3 Pair Of Linear Equations In Two Variables Exercise 3 4




How To Solve 11th Question By Cross Multiplication Method Exercise 3c Solve Each Of The Following Systems Of Equations By Maths Pair Of Linear Equations In Two Variables Meritnation Com
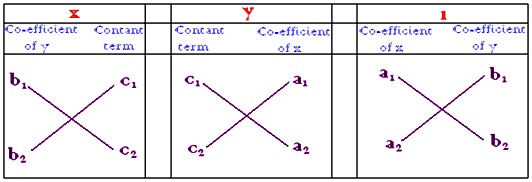



Cross Multiplication Method Formula For Cross Multiplication Linear Equations
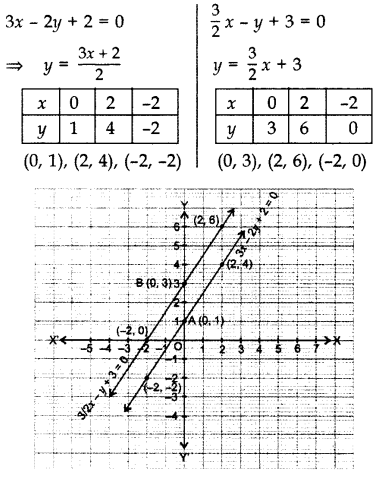



Important Questions For Class 10 Maths Chapter 3 Pair Of Linear Equations In Two Variables Learn Cbse




70以上 3x 2 5y 3 2 X 3 Y 2 13 6 By Elimination Method
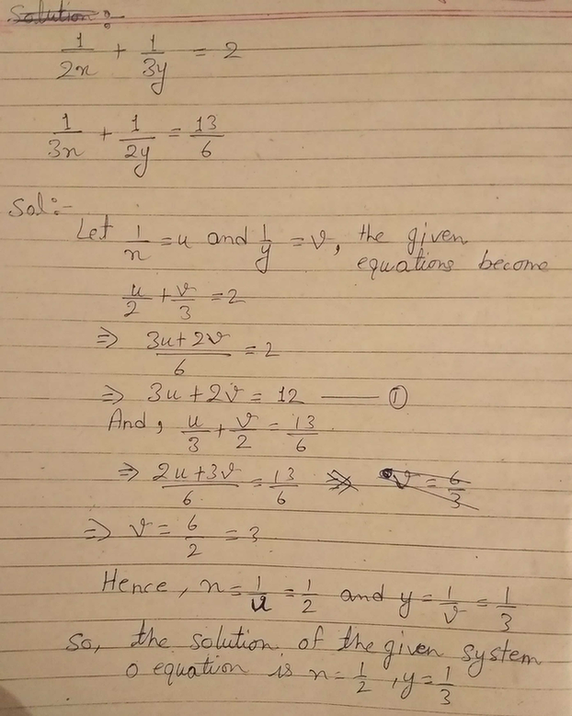



Exercise 3 5 1 Solve The Following Pairs Of Equations By Re Scholr



How To Solve 1 X 1 Y 7 2 X 3 Y 17 Where X And Y Is Not Equal To 0 By Cross Multiplication Method Quora



Solve The Following Pairs Of Linear Equations By The Substitution Method 3x 2 5y 3 2 X 3 Y 2 13 6 Sarthaks Econnect Largest Online Education Community




Solve The Following Pair Of Equations By Cross Multiplication Rule 5x 3y 35 2x 4y 28 Then



Class 10th Maths Chapter 3 Pair Of Linear Equations In Two Variables Notes Ncert Solution Wisdom Academy




How To Solve 11th Question By Cross Multiplication Method Exercise 3c Solve Each Of The Following Systems Of Equations By Maths Pair Of Linear Equations In Two Variables Meritnation Com



Which Of The Following Pairs Of Linear Equations Has Unique Solution No Solution Or Infinitely Many Solutions In Case There Is A Unique Solution Find It By Using Cross Multiplication Method 2x




X Y 3 X 3 Y 2 6 Youtube




Ncert Class 10 Chapter 3 Pair Of Linear Equations In Two Variables




X 2y 2 And X 3y 7 By Cross Multiplication Novocom Top



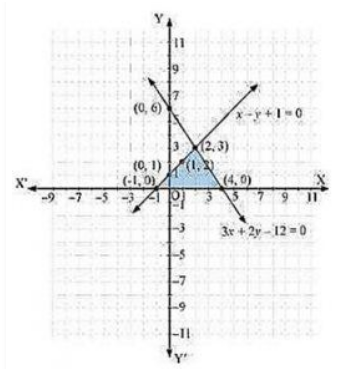
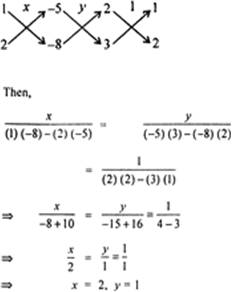
Solve The Following Pair Of Linear Equations By The Substitution Method I X Y 14 X Y 4 Ii S T 3 S 3 T 2 6 Iii 3x Y 3 9x 3y 9 Iv 0 2 X 0 3 Y 1 3 0 4 X 0 5 Y 2 3 V Sqrt 2 X Sqrt 3 Y 0 Sqrt 3 X Sqrt 8 Y 0 Vi 3x 2 5y 2 2 X 3 Y 2 13 6



Pair Of Linear Equations In Two Variables




Which Of The Following Pairs Of Linear Equations Has Unique Solution No Solution Or Infinitely Many Solutions In Case There Is A Unique Solution Find It By Using Cross Multiplication Method 3x




Ex 3 5 3 Solve By Substitution And Cross Multiplication Teachoo




Solve The Given Equations For X And Y By The Method Of Cross Multi



Solve 5 X 1 1 Y 2 2 And 6 X 1 3 Y 2 1 Studyrankersonline




Cbse Ncert Solution For Class 10 Maths Linear Equations In 2 Variables




Gseb Solutions For Class 10 Mathematics Pairs Of Linear Equations In Two Variables Cbse Tuts



1




Simultaneous Linear Equations Class 9th Concise Selina Icse Maths Icsehelp




Cross Multiplication Method Mathematics Satyam




Cbse Ncert Solution For Class 10 Maths Linear Equations In 2 Variables
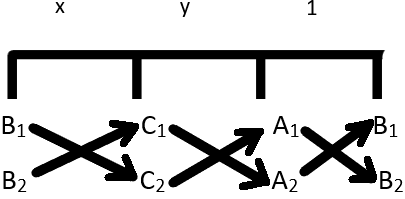



Method Of Cross Multiplication Solve By Method Of Cross Multiplication




Solve The Following System Of Equations By Method Of Cross Mult



Q Tbn And9gcrvxqxwilzvfrimds45eaf0inigyjgztv5jwx 4d0vooqeofoyk Usqp Cau




Ex 3 4 1 Solve By Elimination And Substitution I X Y 5 2x 3y




Chapter 5 Simultaneous Linear Equations Ml Aggarwal Icse Solutions For Class 9 Maths




Solve For X And Y 40 X Y 2 X Y 5 And 25 X Y 3 X Y 1 Mathematics Topperlearning Com Idbi1itt



Solve The System Of Equations By Using The Method Of Cross Multiplication X 6 Y 15 4 0 X 3 Y 12 19 4 0 Sarthaks Econnect Largest Online Education Community
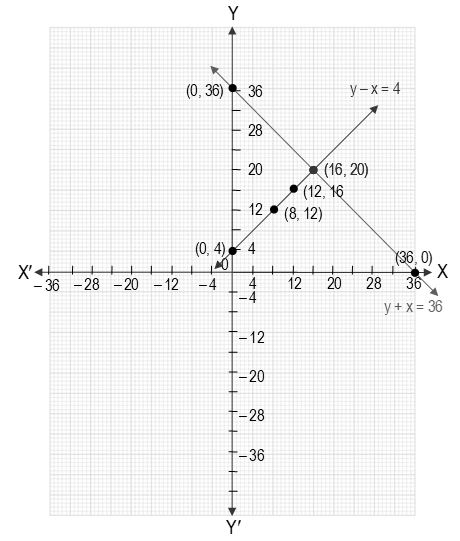



Pair Of Linear Equations In Two Variables




X 3y 7 0 3x 3y 15 0 By Cross Multiplication Method Novocom Top




Mathsmentor Answers Page 30 Ask Truemaths



Solve The System Of Equations By Using The Method Of Cross Multiplication X 6 Y 15 4 X 3 Y 12 19 4 Sarthaks Econnect Largest Online Education Community




Updated Ncert Class 10 Math Pair Of Linear Equations In Two Variables Solution




X Y 3 X 3 Y 2 6 By Cross Multiplication Method Brainly In




R D Sharma Solutions Class 10th Ch 3 Pair Of Linear Equations In Two Variables Exercise 3 4




Ex 3 5 3 Solve By Substitution And Cross Multiplication Teachoo
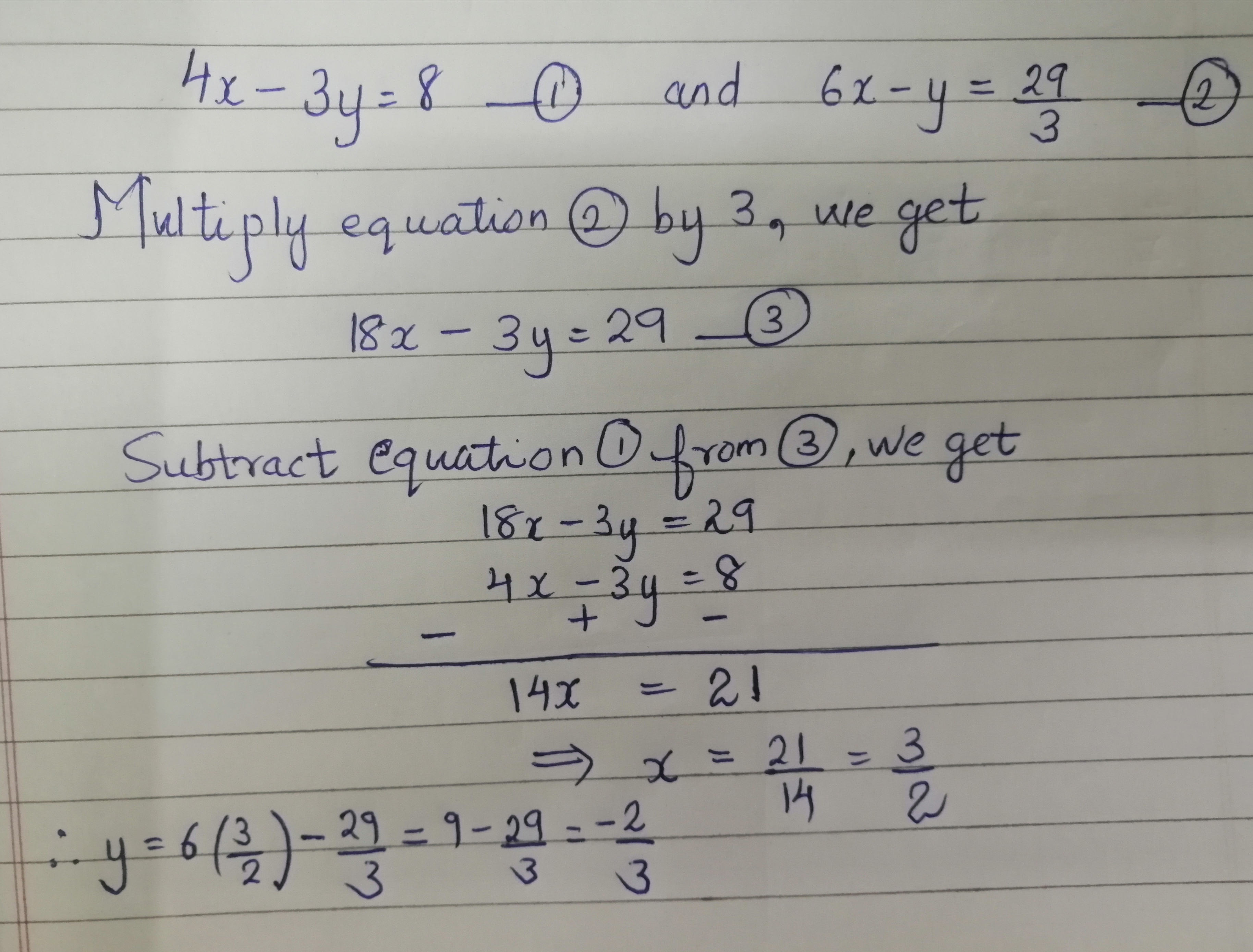



Solve The Sum 4 X Minus 3 Y Is Equal To 8 And 6 X Minus Y Is Equal To 29 Upon 3 By Elimination Of Y Only Mathematics Topperlearning Com 3c9x0inn




Pair Of Linear Equations In Two Variables Equations Cbse Class 10 Ekshiksha




Pair Of Linear Equations In Two Variables Equations Cbse Class 10 Ekshiksha




How To Solve Equations With Three Variables By Cross Multiplication Method Quora




Chapter 3 Pair Of Linear Equations In Two Variables




Solve The Pair Of Equations 2 X 3 Y 13 5 X 4 Y 2 Youtube




Solve The System Of Equations 2x 3y 17 3x 2y 6 By The Meth Scholr



Cbse 10 Math Ncert Solutions




X 7 Y 3 5 X 2 Y 9 6 By Elimination Method Novocom Top


